a phenomenon in laser-induced damage of matter
|
In
laser-induced
damage
experiments,
it is well known
that the threshold fluence, Fth
depends on the number N of pulses
sent
to a single spot on the target material. This phenomenon is
called
material
incubation. In most cases, the threshold fluence decreases
with N starting from the single-shot
ablation
threshold F1
and remains
constant if the pulse number is larger than a critical
saturation
value. If the
fluence is below the multiple pulse threshold F¥,
ablation or damage
does not occur for any number of pulses.
The
first
attempt to model this incubation behavior employed a simple
empirical ansatz of the form Fth,N = F1
× N S-1
[1]. Later, more elaborate models were published. The generic
incubation law
based on our model is of the form:
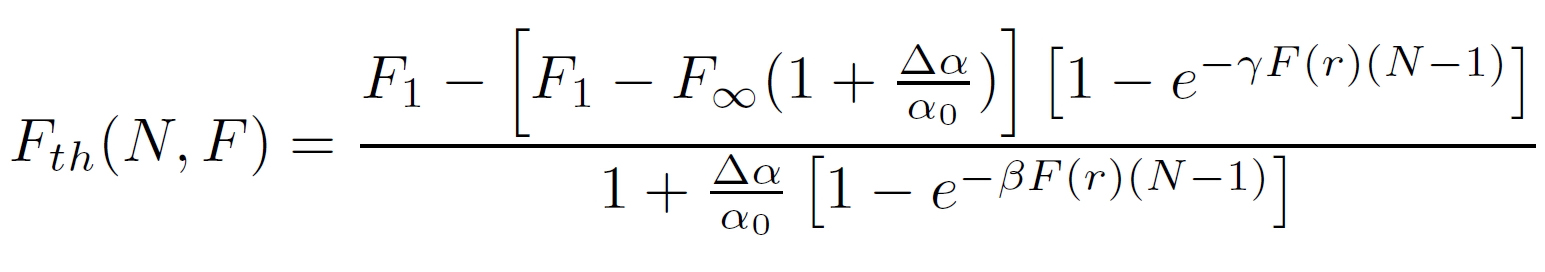 where
a0 is the
initial absorption coefficient of the sample,
Da
is a measure for the change of absorption with every laser
pulse, b is
a material parameter describing the efficiency with which
a
pulse of fluence F
changes the absorption
coeffiecient, while
g is
another
material parameter, describing an efficiency of changing a
critical
ablation
energy with every laser pulse. For details of the model, see
reference
[3]/
You
can
download a MatLab script for fitting the equation above to
your
experimental data here.
Unzip all files into a single directory and run the script IncubationCurveFit.m.
Instructions on how the data
have to be supplied are
contained in the comment section of the script. Please direct
questions
to matthias@lenzner.us
|
Single-shot ablation
thresholds
are often determined by measuring the crater diameter as a
function
of pulse fluence F, as shown in reference [2].
Linear extrapolation of a
plot of the squared diameter D² versus ln(F)
yields the threshold
fluence Fth at D²=0.
The validity of this approach can
be shown easily assuming a Gaussian excitation beam of waist w
and postulating
that ablation occurs within a crater of radius rc
for which
the local incident fluence exceeds the threshold value Fth.
The advantage of this technique is that the measurements can
be
performed at
fluences well above threshold for which the detected
fingerprint
signals are
clearly detectable by far-field microscopy. Also, the beam
radius w
does
not have to be known; it is obtained as slope of the
regression line.
As shown
in reference [3], this method can also be used for multi-pulse
damage
thresholds, the linear interpolation still yields the correct
threshold
fluence Fth,N, however, the
slope might not correspond to the correct
lateral beam dimensions.
You can download a MatLab script for fitting this linear dependence to your experimental data here. Unzip all files into a single directory and run the script DsqFit.m. Instructions on how the data have to be supplied are contained in the comment section of the script. Please direct questions to matthias@lenzner.us |
|
References [1] Y. Jee, M. F. Becker, and R. M. Walser, Journ. Opt. Soc. Am. B 5, (1988) p. 648 [2] J. M. Liu, Opt. Lett. 7, (1982) p. 196 [3] Z. Sun, M. Lenzner, W. Rudolph, Journ. Appl. Phys. 117 (2015) 073102 |
||
| Lenzner Research LLC, 125 E Canyon View Dr, Tucson, AZ 85704, USA, email: info@lenzner.us | ||